Tworzenie pieniędzy z niczego

Sherman K. Stein

Często zastanawiałem się, skąd się biorą pie­niądze. Przecież kiedy powstawały Stany Zjedno­czone, było bardzo mało pieniędzy. Teraz istnieją biliony dolarów. W końcu postanowiłem się tego dowiedzieć i zapytałem się paru profesorów eko­nomii. Ich odpowiedzi były tak dziwne, iż myśla­łem, że robią sobie ze mnie żarty. Przeczytałem więc podręcznik do ekonomii i z zaskoczeniem stwierdziłem, że odpowiedź w nim jest taka sama, jakiej udzielili mi profesorowie. Oczywiście naj­bardziej oczywisty sposób tworzenia dolarów po­lega na tym, iż rząd drukuje banknoty i bije mo­nety. Ale istnieje jeszcze inny sposób tworzenia pieniędzy i – ku mojemu zadowoleniu – wiąże się on z szeregami geometrycznymi. Udział w tym biorą banki.

Okazuje się, że banki mogą tworzyć pieniądze z niczego. I nie ma tu czarów. Sztuczka jest lepsza od fałszowania pieniędzy, i to z dwóch powodów: nie trzeba używać prasy drukarskiej oraz jest cał­kowicie legalna. Polega ona na wierze, jaką ludzie pokładają w przyszłości. Popatrzmy, jak to działa.

Bank musi utrzymywać pewne rezerwy, aby za­spokajać bieżące żądania wypłat posiadaczy kont. Wyobraźmy sobie te pieniądze jako gotówkę w skarbcu. Jeżeli wszyscy posiadacze kont ulegną panice i będą sądzić, że bank wkrótce zbankrutuje, i jeżeli z tego powodu zażądają wypłaty pieniędzy w gotówce, wówczas bank prawdopodobnie nie będzie miał dostatecznych rezerw, aby spełnić te żądania. Bank znajdzie się w kłopotach, a klienci wpadną we wściekłość. Jeżeli jednak taka panika nie występuje, rezerwy banku są wystarczające, aby zaspokoić normalne potrzeby posiadaczy kont.

Niestety niektórzy posiadacze kont tracą wiarę w przyszłość i chcą wycofać pieniądze z Banku Zaufania. Następuje run na bank, czyli panika. Zdarzyło się to podczas Wielkiego Kryzysu, a wówczas rząd federalny w marcu 1933 roku ogło­sił zamknięcie banków. Banki miały usprawiedli­wienie, aby nie wypłacać pieniędzy: były za­mknięte wskutek decyzji rządu. Po kilku tygo­dniach wypłacalne banki otrzymały zezwolenie na otwarcie i stopniowo powróciła wiara w system bankowy.

Na szczęście ludzie zazwyczaj mają zaufanie do swoich banków. Wierzą, że kiedy zechcą wy­płacić swoje pieniądze w gotówce, będą mogli to zrobić. Aby łatwiej podtrzymać tę iluzję, bankierzy ubierają się w tradycyjne garnitury, a architektura banków jest taka, aby wzbudzać zaufanie: podłogi wyłożone granitem, ściany – marmurem, do tego jeszcze kolumny, wszystko przypominające świą­tynię grecką. Bardziej uzasadnione byłoby zapro­jektować bank tak, aby przypomniał kasyno gry w Las Vegas, ale to, oczywiście, zniszczyłoby iluzję.

Zarząd Rezerwy Federalnej wymaga, aby bank utrzymywał pewien ułamek wkładów swoich klientów jako rezerwę, ale resztę może komuś po­życzyć. Dla naszych ce­lów załóżmy, że bank ma obowiązek trzymać jako re­zerwę 20 procent, czyli 1/5, pozostałe 80 procent zaś, czyli 4/5, może komuś pożyczyć. Uważajcie teraz pilnie, bo ja sam nie mogłem w to uwierzyć, póki nie przeczytałem o tym w podręczniku.

Załóżmy, że Jacek przychodzi do Banku Zaufa­nia i wpłaca na konto 1000 dolarów. Bank zatrzymuje 200 dolarów jako rezerwę, a 800 (4/5 z 1000) pożycza Joasi. Joasia wpłaca te 800 dolarów do tego samego albo do innego banku. Bank ten zatrzymuje 20 procent z 800 dolarów jako rezerwę, a 640 dolarów (4/5 z 800) pożycza Alicji.

Już się zaczęły czary: Jacek sądzi, że posiada 1000 dolarów, Joasia sądzi, że posiada 800, a Ali­cja sądzi, że posiada 640. Na początku było tylko 1000 dolarów Jacka. Teraz, zupełnie znikąd, jest łącznie 1000 + 800 + 640 = 2440 dolarów. Niezła sztuczka, prawda? Co więcej, bank zarabia prowi­zję i odsetki od stworzonych w ten sposób pienię­dzy. Jest oczywiste, że banki to bardzo korzystny interes.

Teraz załóżmy, że Alicja wpłaca do banku swoje 640 dolarów. Bank pożycza 512 dolarów (4/5 z 640) Leszkowi. Leszek z kolei wpłaca 512 dolarów, dzięki czemu Bank Zaufania ma prawo udzielić pożyczki na 409,60 dolara (4/5 z 512) Magdzie. I tak dalej, i tak dalej. Obliczmy, ile wy­niesie łączna ilość pieniędzy, jeśli tak to będzie szło przez dłuższy czas: wpłata, pożyczka, wpłata, pożyczka itd. Czy jest możliwe, aby w ten sposób stworzyć nieskończoną ilość pieniędzy? Zaraz zo­baczymy.

Proces zaczyna się od 1000 dolarów. Następ­nie jest 800, czyli 4/5 z 1000. Potem jest 640, czyli 4/5 z 800. Inaczej:

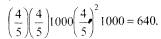
Następnie jest 512 dolarów, czyli 4/5 z tej kwoty, a więc:

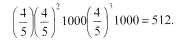
W każdym kroku kwota jest 4/5 razy mniejsza niż kwota w kroku poprzednim. A zatem całkowita ilość pieniędzy posiadana przez ludzi jest sumą nieskończonego szeregu:

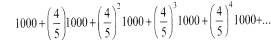
Na poniższym rysunku zilustrowano uczestni­czące w tym procederze stosy pieniędzy.

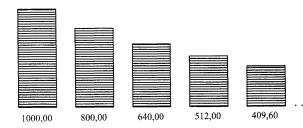
Chcemy się dowiedzieć, czy suma ta jest skoń­czona czy nieskończona. A jeżeli jest skończona, to ile wynosi? Po wyciągnięciu przed nawias wspólnego czynnika 1000, otrzymujemy:

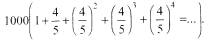
Suma w nawiasach jest szeregiem geometrycz­nym. Suma tego szeregu wynosi:

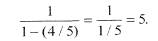
Oznacza to, że łączna ilość pieniędzy, jakie Ja­cek, Joasia, Alicja, Leszek i Magda i tak dalej w swoim mniemaniu posiadają, wynosi 1000 x 5 = 5000 dolarów. (Ekonomiści nazywają ten czynnik, w naszym przypadku 5, mnożnikiem kreacji pie­niądza. Mnożnik ten zależy od ułamka wkładów, jaki musi być utrzymywany w charakterze re­zerwy. Dokładniej biorąc, mnożnik jest odwrotno­ścią tego ułamka).

Tak więc na początku mieliśmy 1000 dolarów, a po dłuższym czasie będziemy mieli z tego 5000. Pocieszające jest jedynie to, że Bank Zaufania nie może stworzyć nieskończonej ilości pieniędzy z 1000 dolarów. Wyczarował znikąd tylko 4000.

Jeden z czytelników tego, co tu napisałem my­ślał, że wszystko to jest satyrą. „Przecież ostatecz­nie pożyczki bankowe muszą zostać spłacone, i to z procentem". Owszem, pożyczki są spłacone, ale pieniędzmi tworzonymi w opisany przeze mnie sposób. Kto nie wierzy, niech przeczyta jakikol­wiek podręcznik ekonomii.

Można też inaczej spojrzeć na zamianę 1000 dolarów w 5000 dolarów. Niepotrzebny tu będzie szereg geometryczny. Musimy jednak teraz zało­żyć, że całkowita ilość pieniędzy jest skończona. Jest to silne założenie. Przy użyciu szeregu geo­metrycznego nie musieliśmy tego zakładać.

Oznaczamy całkowitą ilość pieniędzy przez T. Ponieważ jest to liczba skończona, możemy na niej wykonywać działania arytmetyczne i algebraiczne. (Jak wiedzieliśmy, liczba ta wynosi 5000, ale uda­wajmy, że tego nie wiemy). Na T składa się po­czątkowa wpłata 1000 dolarów i wszystkie wpłaty wykonane później. Nazwijmy te późniejsze wpłaty wpłatami wtórnymi. Każda wpłata wtórna wynosi 4/5 wpłaty poprzedniej. Zilustrowane jest to na poniższym rysunku.

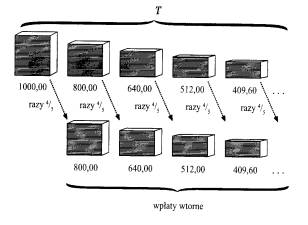
Suma wszystkich wpłat wtórnych wynosi 4/5 T (ponieważ każda wpłata wtórna wynosi 4/5 od­powiedniej wpłaty, składającej się na T). A zatem całkowita suma wpłat T jest sumą początkowej wpłaty 1000 dolarów i wszystkich wpłat wtórnych 4/5 T. Inaczej:

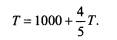
Pozostaje zatem tylko rozwiązać to równanie z niewiadomą T.

Ponieważ nie lubimy mianowników, mno­żymy obie strony przez 5 i otrzymujemy

5T = 5000 + 4T.

Teraz odejmujemy 4T od obu stron i otrzymu­jemy

T = 5000.

Tak więc w sposób pośredni wyznaczyliśmy sumę wszystkich wpłat, wykazując że wynosi ona 5000 dolarów. Oznacza to, że wykazaliśmy, iż

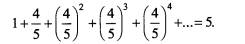
Inaczej mówiąc, Bank Zaufania pozwolił nam spojrzeć w inny sposób na szereg geometryczny. Jest to nie mniej czarodziejskie, niż wytwarzanie pieniędzy z niczego. (Metoda ta jest dobra dla każdej liczby r pomiędzy 0 a 1, nie tylko dla 4/5. Jednak pamiętajmy, że przy takim podejściu mu­sieliśmy z góry założyć, że suma T jest liczbą skończoną).

Być może ktoś z was zastanawia się teraz: „Czy mogę założyć bank?" Zapytajcie profesorów ekonomii. Powinni wam polecić jakiś podręcznik.

Sherman K. Stein

Sherman K. Stein jest profesorem matematyki Univer­sity of California w Davis. Artykuł jest rozdziałem książki Strength in Numbers (wyd. pol­skie Potęga liczb, wyd. Amber, Warszawa 1998)